解析2:その他ファイルの取得
音楽ファイルとは別にもう一つファイルサイズが大きいファイルが存在します。
他にファイルサイズが大きいファイルが存在しない、exeファイル自体も非常に小さい、などからこれがその他の画像ファイルや効果音などなどを内部に保持していると見て間違いなさそうです。
とりあえず前回と同じようにバイナリエディタで開いてみることにします。

なにやら凄い見覚えがある並び方をしているのが見て取れると思います。
どうやら音楽ファイルと同じ形式でファイルリストを保持しているようなので、試しに前回作ったツールで展開してみることにします。
予想通り展開できました、ですが展開できたファイルを開こうとしても開くことが出来ません。
試しに出来たファイルをバイナリエディタで開いてみると
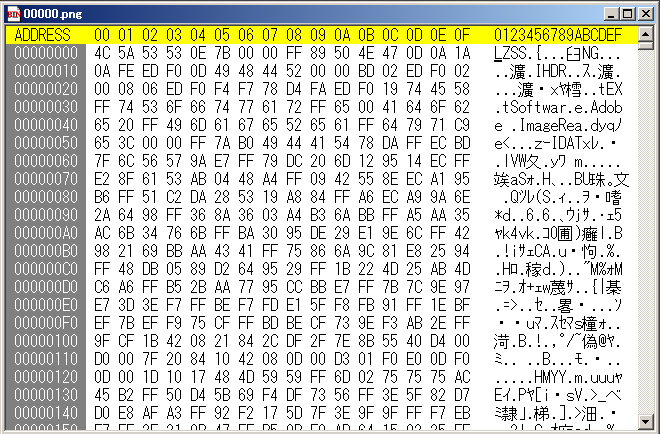
0x09に見える臼NGというのがpngの識別子です(正確にはその後の4byteも含みます)
他のファイルを開いても全て最初4byteがLZSSであることと、PNGの識別子が直接確認できることからなにかしら圧縮がかかっていると推測できますね。
ここでまず冒頭4byteに書かれているLZSSについて説明します。
(正式な仕様書の類を見たわけではなく全てコードを読んだ経験からきている知識のため、一部間違えている可能性があります)
軽く検索をかければ判ることですが、LZSSというのは有名な圧縮アルゴリズムの一種で
動的に辞書を作り、距離と長さをあらわすデータに遭遇したら辞書中の距離位置のデータを長さだけ取り出して展開先データとするものです。
(詳細についてここで詳しく述べることはありませんので自分で調べてください)
このアルゴリズム自体ポピュラーなもので、割と色々な実装が行われているためLZSSだとわかっただけでは具体的な展開方法まではわかりません。
そこでまず、バイナリから可能な限り情報を引き出すことにします。
第一に、このソフト上で実装されているLZSSはバイト単位で管理されていることがわかります。
通常であればビット単位で一致不一致を示すフラグ1bit、その後一致であれば距離と長さを表すデータ、不一致であれば元データ1byteという流れになるため
バイナリエディタ上で元データを一部でも読み取れるはずがありません。
なので、一致不一致を示すbit列はどこか一箇所にまとめてあるか、byte単位で表現されていると推測されます。
次に0x08番地に存在する0xFFについて、上の画像だけではわかりませんがほぼ全てのファイルにおいてそこが0xFFで固定でした。
また、png以外にもテキストファイルを含んでいたのですが、そのテキストファイルを見る限り0xFFのあと8byteは必ず元データがそのままという流れになっているようです。
さらに0x31~0x3A番地に注目してください、ここはおそらくtSoftwareという文字列が元データだと推測できますが、間に0xFFという余分な情報が挟まれているのがわかります。
まず0x39番地の余分な1byteはそのままつなげるだけで復元可能な点から、間の0xFFが距離と長さを示す情報以外のデータだと推測できます。
LZSSにおいて他に存在しうるデータといえば、辞書サイズか一致不一致フラグのみですが
辞書サイズがデータ上に点在している可能性は非常に低いため、この1byteが一致不一致フラグであると推測できます。
次に0xFFの後必ず元データが8byte並ぶことから8つ分の不一致をあらわす情報だと仮定することが出来ます。
それは0x08番地が固定である事からも読み取ることが可能で、辞書にデータが存在しない初期の状態では必ず不一致バイトが来ることが推測できるからです。
これらのことから、一致不一致フラグを8つまとめることでbit入出力を減らして効率化しているであろうことが推測できました。
(0x9Fの場合一致5不一致2一致1となるので、元データ5byte距離長さデータが2つ最後に元データ1byteとなります)
現時点では推測に推測を重ねる形ですが、試しにそうであると仮定して0xFF以外のフラグに遭遇するまで展開するコードを書いてみれば問題なく取れているが判ります。
また、0xFF以外のフラグに遭遇した後のデータを並べてみれば、その後2byte元データとは違うデータが混じっていることがわかりました。
これはやはり一致不一致フラグを8つまとめたものであり、さらに距離と長さを示す情報は2byteであろうことも推測できます。
この時点で一致フラグを無視し、不一致分だけ全て読み出すものを作りました。
png画像に用いてもいまいち結果がわかりませんが、テキストデータはNULL文字を含まない形に展開できたためここまでは推測が当たっていることが判ります。
次に必要になってくるのが辞書の作成方法と辞書サイズです。
辞書サイズは大きく分けて固定サイズ、ファイル内に保持している、ファイルサイズから算出の三方式があります。
ですが、ファイルサイズから算出であれば距離を表現するのに使うビット数が可変になるため現在のように2byte固定はありえません、なので算出では無いでしょう。
次にファイル内に保持している可能性として0x04番地の値が思い浮かびますが、必ずファイルサイズ以上の値を保持している、距離と長さを表現するバイト数は2byteであるため辞書サイズも最大で2byteである点からおそらくは違うでしょう。
というわけで、現在は固定サイズであると仮定して先に進みます。
細かい説明は省きますが、pngはフォーマットの使用上原則的に16byte目まで固定です。
(ほぼ確実に89 50 4E 47 0D 0A 1A 0A 00 00 00 0D 49 48 44 52となる)
なので2枚目の画像の0x11~0x13番地のFE ED F0の部分については展開後の様子が推測可能になります。
まず0x11番地の0xFEは一致不一致フラグで2進数に直すと11111110となるので0x12~0x13番地の2バイトが距離と長さを示す情報です。
次に展開先のデータですが、00 00 00 0Dで次の不一致データが0Dであるため00が3byte続く形に展開されると推測できます。
ですが、そこまでの12byteを見ても00が1byteも存在しません。
LZSSには良く使われる手法の一つに、事前に登場しやすいバイト列を辞書登録しておくことで圧縮効率を上げるというものがあります。
さらにその中で一番使われているのが辞書全体を00で埋めておくというもので
今回もその例であると推測可能です。
なので、既に辞書登録されているデータの前後どちらかとなるので登録済み12byte+長さ3byte分前の指定で15、もしくは直後指定で0だと仮定できます。
他にも辞書中を相対的に参照する距離ではなく絶対座標として参照する方式もありますが、現時点では推測不可能であるため無視することにします。
次に長さですが、使用するバイト数以下の長さでは置き換えても無駄であるため
基本的に置き換え必要バイト長+1が長さの最低値となります。
なので、長さ0をこの最低値として定義することで最低値分だけ長い一致まで表現することが可能になります。
(長さに1byte割り振った場合、そのままでは長さ255までしか格納できないが最低値を3と定義すると長さ258まで格納できる)
今回の場合は置き換えに2byte使用しているので、この手法が用いられていれば最低値3になります。
つまり今回は3byteなのでそのまま3か圧縮されて0だと仮定できます。
上記のことを踏まえてED F0の部分を眺めてみます。
まず、ビット列に戻すと1110 1101 1111 0000という並びになります。
この時点でまず1が出現する最多組み合わせである15 3よりも1が多い事に気づけます。
なので、距離か長さもしくは両方の推測が外れているとわかります。
現在考えられる可能性といえば、距離が相対ではなく絶対座標製である可能性です。
私自身理由が良くわかっていないのですが、絶対座標方式の場合辞書登録の始点が0x00番地からではないことが多いです。
なので、今回の例についても格納されているであろう数値が推測できません。
(それが目的の可能性もありますが、暗号化を目的としない圧縮アルゴリズムであるため可能性は低いと考えられます)
まず、効率化の観点から距離長>長さ長になることは確実なので、今回の例で言えば少なくとも距離長に10bitは割り振られていると考えられます。
それを踏まえてどちらか該当しないかと考えれば、辛うじて後半4byteが長さを表現しているのではないかと推測できます。
この時点で距離長が12bitと推測できるため、12bitで表現しうる最大値0xFFF+1=0x1000が辞書サイズであるという仮定も成り立ちます。
またbit入出力をなくすなど演算速度を重視していることから単純に2byte目の上位4bitを1byte目の前か後につなげる形だと思われるので0xFEDか0xEDFが距離であると考えられます。
もし距離が0xFEDであるならば、登録データ前を参照していた場合は0xFED+3で始点0xFF0、後を参照していた場合は0xFED-12で始点0xFE1。
0xEDFであれば前参照で0xEE2、後参照で0xED3。
現時点まで全ての推測が正しい場合はこの4パターンのどれかで展開できることになります。
ここまで来れば後は簡単で、実際に実装してみて4パターン全て試してみることにします。
格納されていたファイル自体多いので全て同じように調べて回ればどれか一つに絞り込めるかもしれませんが、実際検証した方が早いのでコードを組んでみることに。
結果としてみごと辞書始点0xFF0で展開に成功しました。
上の文章だけ読むと適当な推測を積み重ねていったら運良く正解にたどり着けただけのように思えるかもしれませんが、実際そのとおりです。
ただし上記の10倍程度は推測を重ね、その全てで失敗した結果この結論にたどり着いた形になります。
一例を挙げるならば、過去に登場していない0x00の3byteが圧縮されているという部分
ここで私は最初LZSSだけではなくランレングス圧縮も併用されており、距離と長さデータだと思っていた部分のうち1bitをフラグにして一部ランレングスとして機能しているのではないか?と考えました。
上記のとおりそんなことは無かったのですが、最初はそうとしか思えずランレングスの実装例をいくつもあさったものです。
結果として、本来であればデバッガーやメモリーエディターの力を借りておそらく3時間程度で済む解析に丸2日かけた計算になります。
やはりデバッガーは偉大だなと思いつつ、ランレングスやLZSSについてそれなりの知識を得られたので悪い試みではなかったと思っています。
もう一度やりたくはないですが……
ちなみに、今回と前回であげた例は非常に簡単な部類です。
本来であればバイナリエディタで見た時点でまっとうに意味を理解できる文字列が存在していること自体珍しく、デバッガーの力なしでは解析の足がかりにさえたどり着けないことも多いです。
最終的には上記と同じ道筋を辿るとはいえ、一般的な解析ではまず砂漠から一本の針を探すような途方もない作業が待っており、上記解析過程にたどり着いた時点で勝ちといっても過言ではありません。
そういう意味では、今回の記事は解析過程と銘打つには少々的外れな内容だったのかもしれませんね。
というわけで、解析過程の解説記事はこれで終了となります。
もしこのような奇特な記事を最後まで読んだ方がいるならありがとう、そしてお疲れ様でした。